Rumus asli phytagoras
Membuktikan kebenarannya, di mulai dengan membuat gambar sebuah persegi besar, kemudian gambarlah sebuah persegi kecil di dalam persegi besar tersebut, seperti gambar berikut:
Perhitungannya :
Luas persegi besar = Luas persegi kecil + 4 Luas segitiga
( b + a ) . ( b + a ) = c . c + 4 . 1/2 b.a
b2 + 2 b.a + a2 = c2 + 2 b.a
b2 + a2 = c2 + 2 b.a - 2 b.a
b2 + a2 = c2
---------------------------------------------------------------
Anda pasti tak asing lagi dengan rumus ini. Rumusnya sebagai berikut:
a2 + b2 = c2a adalah sisi alas (horizontal), b adalah sisi tinggi (vertikal), sedangkan c adalah sisi miring. Untuk lebih jelasnya bisa dilihat pada gambar ini.
Bagaimana? Sudah jelas kan?
Untuk mencari masing-masing sisi digunakan rumus berikut:
Untuk mencari a:
a = √(c2 - b2)
Untuk mencari b:
b = √(c2 - a2)
Untuk mencari c:
c = √(a2 + b2)
Contoh soal:
Sebuah segitiga siku-siku dengan sisi alas 5 cm dan sisi tinggi 12 cm. Berapakah sisi miringnya?
Jawab:
Diketahui:Contoh soal lainnya:
a = 5 cm
b = 12 cm
Ditanya:
c = ?
Penyelesaian:
c = √(a2 + b2)
c = √(52 + 122)
c = √(25 + 144)
c = √169
c = 13
Jadi, sisi miringnya adalah 13 cm.
Sebuah segitiga siku-siku dengan garis alas 9 cm dan garis miring 15 cm. Berapakah kelilingnya?
Jawab:
Diket:
a = 9 cm
c = 15 cm
Dit:
k = ?
Peny:
Mula-mula, kita harus mencari sisi tinggi (b) dulu.
b = √(c2 - a2)
b = √(152 - 92)
b = √(225 - 81)
b = √144
b = 12
Lalu, karena b sudah ditemukan, maka kita bisa mencari kelilingnya.
k = a + b + c
k = 9 + 12 + 15
k = 36
Jadi, keliling segitiga tersebut adalah 36 cm.


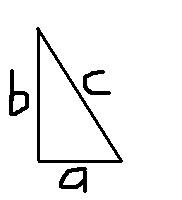
Tidak ada komentar:
Posting Komentar