RUMUS LUAS SEGITIGA

Jika anda ingin mencari luas segitiga intinya anda harus mengetahui panjang alas dan tinggi segitiga tersebut. Yang dimaksud dengan alas adalah panjang bagian bawah segitiga jika segitiga tersebut ditegakkan dengan sudut siku 90 derajat. 

 

Tinggi segitiga adalah panjang bagian sisi tegak lurus 90 derajat terhadap alas. Secara umum rumus luas segitiga adalah 1/2 x alas x tinggi.

 

 Untuk beberapa jenis segitiga lain maka rumus umum tersebut dapat dikembangkan lebih lanjut.

I. RUMUS UMUM LUAS SEGITIGA

Segitiga Siku

Dari segitiga siku-siku di atas maka yang dimaksud dengan sisi alas adalah b, tinggi adalah a dan sisi miring adalah c. Maka persamaan dari rumus segitiga di atas adalah :

Dik : 

a = sisi tinggi

b = sisi alas

c = sisi miring

Dit : L (luas segitiga) ?

Maka,

L = 1/2 a b

Ingat rumus luas segitiga di atas hanya berlaku jika segitiga mempunyai sudut siku-siku ( 90 derajat ). Perhatikan bentuk segitiga di atas dan coba amati persamaan rumusnya. 

 

Jika anda jeli maka anda dapat menarik kesimpulan bahwasanya utntuk mencari luas segitiga siku seperti di atas sama halnya dengan mencari setengah luas dari empat persegi panjang. Anggap saja panjang dari empat persegi panjang tersebut adalah b dan lebar adalah a, luas persegi panjang adalah a x b.

 

 Karena segitiga tersebut adalah mempunyai luas sebesar setengah kali dari luas persegi panjang maka didapatlah formula 1/2 x alas x tinggi.

 

 

II. RUMUS LUAS SEGITIGA SAMA KAKI

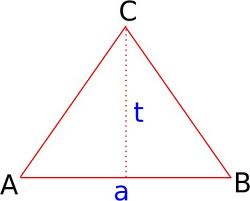Segitiga Sama Kaki

Untuk mencari luas segitiga sama kaki sebenarnya kita menggunakan rumus yang sama dengan rumus luas untuk segitiga siku. Hanya saja pada segitiga sama kaki tingginya bukan salah satu sisi segitiga tetapi adalah garis tengah yang membelah kedua kaki segitiga dan tegak lurus terhadap alas. 

 

Sehingga segitiga tersebut seperti terbelah dan mendapatkan dua buah segitiga siku. Jadi dapat kita simpulkan bahwa rumus luas segitiga sama kaki adalah alas x tinggi. Yang dimaksud dengan alas pada gambar di atas adalah panjang AB. Maka persamaan untuk rumus luas segitiga sama kaki tersebut di atas adalah :

Dik : Segitiga sama kaki ABC

alas = Panjang AB = a
tinggi = panjang garis tegak = t

Dit : L (luas segitiga) ?

Maka,
L = a x t

atau,

L = 2 x (1/2 a x t), rumus ini didapat jika anda mencari luas salah satu segitiga sama kaki yang dibelah. Setelah luas salah satu segitiga didapat maka karena ada dua segitiga yang sama, anda tinggal mengalikan dengan 2.

Untuk mencari tinggi segitiga sama kaki anda dapat menggunakan rumus pitagoras (pythagoras) yakni:

panjang b kuadrat adalah akar dari pengurangan c kuadrat dengan a kuadrat. Dimana a : alas, b : tinggi dan c : sisi miring. Rumus pitagoras ini juga hanya berlaku jika segitiga tersebut adalah segitiga siku-siku.

 

 

III. RUMUS LUAS SEGITIGA SAMA SISI

Segitiga Sama Sisi

Pada segitiga sama sisi sebenarnya rumus yang digunakan adalah sama saja dengan rumus pada segitiga sama kaki. Yaitu kita mencari tinggi terlebih dahulu kemudian baru bisa dicari luasnya. 

 

Tetapi sekarang sudah ada beberapa cara cepat yang ditemukan agar tidak banyak menghabiskan waktu mencari tinggi terlebih dahulu.

 

 Pada kesempatan ini saya tidak akan membahas mengenai cara cepat tersebut, cara cepat untuk mencari luas segitiga sama sisi bisa anda pelajari pada bimbingan belajar-bimbingan belajar yang sekarang sudah banyak di kota-kota besar.

Dari gambar segitiga sama sisi di atas maka dapat ditentukan rumus luasnya adalah :

Dik :

s = sisi ketiga sisi segitiga

t = tinggi

Dit : Luas segitiga /

L = s x tinggi

atau

 

 

IV. RUMUS LUAS SEGITIGA SEMBARANG

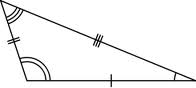Segitiga Sembarang

Untuk mencari luas segitiga sembarang maka sudah barang tentu akan berbeda dengan rumus yang digunakan pada beberapa jenis segitiga sebelumnya.

 

 Ini karena tidak ada sudut siku pada ketiga sudut segitiga. Sehingga kita tidak dapat menentukan tingginya. Tapi rumus umum tersebut bisa saja diterapkan dengan kondisi tertentu. 

 

Misalnya ada beberapa sisi dan sudut besarnya diketahui serta ditetapkan garis tinggi yang tegak lurus membentuk sudut siku.

Agar anda tidak menghabiskan waktu dalam mencari luas segitiga sembarang, maka anda bisa menggunakan rumus yang telah ditemukan dan dibakukan oleh ahlinya dan rumus segitiga sembarang ini disebut teorama heron. Berikut persamaan dari teorama heron :

Dik :

a, b, c = ketiga sisi segitiga

Dit :

Luas Segitiga ?

Maka,

  

 

 

 

Untuk beberapa kondisi lainnya untuk mencari luas segitiga anda bisa juga menerapkan rumus trigonometri. Tetapi harus ada salah satu atau lebih sudut yang besarnya diketahui. 

 

Mungkin jika anda seorang yang maniak dengan matematika, anda bisa menentukan rumus luas segitiga anda sendiri yang mungkin menurut anda lebih mudah dan cepat.